Fonctions Hyperboliques dans Excel – GUIDE COMPLET

Les fonctions hyperboliques dans Excel jouent un rôle crucial dans des domaines tels que l'analyse financière, l'ingénierie et la recherche scientifique. Ces fonctions, moins connues que leurs homologues trigonométriques, offrent pourtant des perspectives uniques dans le traitement et l'analyse de données complexes.

Excel, avec ses fonctionnalités avancées, est parfaitement équipé pour exploiter la puissance des fonctions hyperboliques.

Pourquoi utiliser les Fonctions Hyperboliques dans Excel

Avant de plonger dans les détails, explorons pourquoi Excel est l'outil idéal pour les calculs hyperboliques…

• Analyse de Données Avancée: Excel facilite le maniement de vastes ensembles de données. Les fonctions hyperboliques permettent d'analyser des phénomènes complexes, comme la croissance exponentielle ou les modèles de dégradation.
• Visualisation des Données: Grâce à ses outils graphiques, Excel aide à visualiser les comportements hyperboliques, rendant les interprétations plus intuitives.
• Applications Diverses: Ces fonctions sont essentielles dans des domaines variés, comme la modélisation économique, l'étude des ondes électromagnétiques, ou encore dans certains calculs actuariels.
• Accessibilité et Simplicité: Excel rend l'application de concepts mathématiques avancés accessible à tous, grâce à une interface utilisateur intuitive.
  En résumé, Excel transcende son rôle de simple tableur pour devenir un outil de modélisation mathématique avancée, rendant les fonctions hyperboliques pratiques et accessibles.

Introduction aux Fonctions Hyperboliques de Base dans Excel

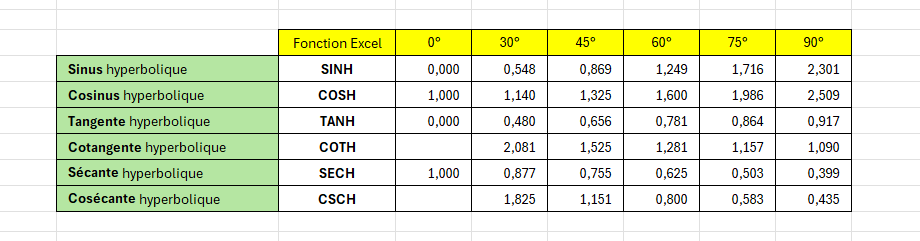
La trigonométrie hyperbolique, une branche captivante des mathématiques, étudie les relations entre les côtés d'un triangle hyperbolique. Ces fonctions hyperboliques – COSH, SINH, TANH, COTH, SECH et CSCH – sont les piliers fondamentaux pour la compréhension des phénomènes exponentiels et hyperboliques dans Excel.

Ces fonctions calculent avec les valeurs en radians. Si vous voulez faire vos calculs en degrés, vous devrez combiner les fonctions hyperboliques avec la fonction RADIANS.

Fonction Excel COSH (cosinus hyperbolique)

• Syntaxe: =COSH(nombre)
• Description: Calcule le cosinus hyperbolique d'un nombre (en radians).
• Exemple: =COSH(1) renvoie environ 1,54. Pour 45 degrés: =COSH(RADIANS(45)) on obtiendra la valeur de 1,33.

Fonction Excel SINH (sinus hyperbolique)

Syntaxe: =SINH(nombre)
Description: Détermine le sinus hyperbolique d'un nombre (en radians).
Exemple: =SINH(1) donne environ 1,18. Pour 30 degrés: =SINH(RADIANS(30)) on obtiendra la valeur de 0,55.

Fonction Excel TANH (tangente hyperbolique)

Syntaxe: =TANH(nombre)
Description: Renvoie la tangente hyperbolique d'un nombre (en radians).
Exemple: =TANH(1) résulte en environ 0,76.

Fonction Excel COTH (cotangente hyperbolique)

Syntaxe: =COTH(nombre)
Description: Renvoie la cotangente hyperbolique d'un nombre (en radians).
Exemple: =COTH(1) résulte en environ 1,31.

Fonction Excel CSCH (cosécante hyperbolique)

Syntaxe: =CSCH(nombre)
Description: Calcule la cosécante hyperbolique d'un nombre (en radians).
Exemple: =CSCH(1) pour la cosécante hyperbolique de 1.

Fonction Excel SECH (sécante hyperbolique)

Syntaxe: =SECH(nombre)
Description: Renvoie la sécante hyperbolique d'un nombre (en radians).
Exemple: =SECH(1) pour la sécante hyperbolique de 1.

Comprendre et Utiliser les Fonctions Hyperboliques Inverses

En ce qui concerne les fonctions inverses, Excel propose directement des fonctions dédiées pour les inverses hyperboliques – ACOSH, ASINH, ATANH et ACOTH. Pour l'arc sécante hyperbolique et l'arc cosécante hyperbolique, il est possible de les calculer en utilisant des formules basées sur ACOSH et sur ASINH.

Le résultat de ces fonctions est en radians. Si vous souhaitez voir le résultat en degrés, il vous faudra ajouter à la formule la fonction Excel DEGRES.

Fonction Excel ACOSH (cosinus hyperbolique inverse)

Formule: =ACOSH(nombre)
Description: Calcule le cosinus hyperbolique inverse d'un nombre.
Exemple: =ACOSH(2) aura comme résultat environ 1,32 radians. Si vous souhaitez le résultat en degrés: =DEGRES(ACOSH(2)) vous donnera environ 75,5°.

Fonction Excel ASINH(cosinus hyperbolique inverse)

Formule: =ASINH(nombre)
Description: Détermine le sinus hyperbolique inverse d'un nombre.
Exemple: =ASINH(0,5) ce qui résultera en 0,48 radians.

Fonction Excel ATANH(cosinus hyperbolique inverse)

Formule: =ATANH(nombre)
Description: Calcule la tangente hyperbolique inverse d'un nombre.
Exemple: =ATANH(0,75) résultera en 0,97 radians et =DEGRES(ATANH(0,75)) en 55,75 degrés .

Fonction Excel ACOTH(cosinus hyperbolique inverse)

Formule: =ACOTH(nombre)
Description: Calcule la tangente hyperbolique inverse d'un nombre.
Exemple: =ACOTH(5) vous donnera 0,2 radians et =DEGRES(ACOTH(5)) résultera en 11,62 degrés.

Calcul de la Sécante hyperbolique inverse dans Excel

Calcul à utiliser: =ACOSH(1/nombre)
Description: Calcule la tangente hyperbolique inverse d'un nombre.
Exemple: =ACOSH(1/0,3) va donner comme résultat de la sécante hyperbolique inverse 1,87 radians. Ainsi =DEGRES(ACOSH(1/0,3)) va vous donner environ 107,36 degrés.

Calcul de la Cosécante hyperbolique inverse dans Excel

Calcul à utiliser: =ASINH(1/nombre)
Description: Calcule la tangente hyperbolique inverse d'un nombre.
Exemple: =ASINH(1/0,5) pour renverra la cosécante hyperbolique inverse d'environ 1,44 radians. =DEGRES(ASINH(1/0,5)) de son côté renverra comme résultat environ 82,71 degrés.

Applications réelles des Fonctions Hyperboliques d'Excel

Les fonctions hyperboliques dans Excel sont particulièrement utiles dans des situations où les modèles de croissance ou de dégradation sont exponentiels ou hyperboliques. Elles sont largement utilisées dans des domaines tels que:

• Analyse Financière: Modélisation de la croissance des intérêts composés.
• Physique et Ingénierie: Étude des ondes électromagnétiques et des courbes de lumière en optique.
• Mathématiques Appliquées: Dans la résolution d'équations différentielles ou lors de l'analyse de séries temporelles.

Éviter les Pièges – Conseils d'Expert sur les Fonctions Hyperboliques dans Excel

L'utilisation efficace des fonctions hyperboliques nécessite une attention particulière:

• Conversion en Radians: Veillez à convertir les angles en radians avant d'utiliser ces fonctions. Utilisez la fonction RADIANS pour cette conversion.
• Conversion en Degrés: Idem pour la conversion des résultats qui sont en radians. Pour passer aux degrés, servez-vous de la fonction DEGRES (voir les exemples plus haut).
• Gestion des erreurs: Comme pour toute fonction mathématique, assurez-vous que les valeurs saisies sont valides pour éviter des erreurs.
• Compréhension des limites: Les fonctions hyperboliques inverses nécessitent une compréhension de leurs limites et domaines pour éviter des résultats incorrects.

Conclusion – Maîtriser la Trigonométrie Hyperbolique dans Excel

Nous avons exploré les fonctions hyperboliques dans Excel, un domaine souvent négligé mais riche en possibilités. En les maîtrisant, vous pouvez aborder des calculs complexes avec confiance et précision, ouvrant ainsi de nouvelles perspectives dans vos analyses et modélisations.

Pour aller plus loin en Excel

Pour terminer, je vous propose d'autres articles sur Excel-Malin.com qui pourraient vous être utiles…

• Liste de toutes les plus de 502 fonctions disponibles sur Excel
• Excel Online Gratuit – comment ça marche
• Grand Tutoriel: Tableaux Croisés Dynamiques Excel
• Calculer l'âge actuel en Excel