Fonctions Trigonométriques dans Excel – GUIDE COMPLET

Les fonctions trigonométriques dans Excel ne sont pas seulement des outils mathématiques; elles sont des passerelles vers une analyse plus approfondie et une meilleure compréhension de divers phénomènes et données. Que vous soyez étudiant, ingénieur, analyste financier, architecte ou simplement un passionné de mathématiques, la maîtrise de ces fonctions ouvre un monde de possibilités.

Excel, avec sa flexibilité et sa facilité d'utilisation, est l'outil idéal pour explorer la trigonométrie.

Pourquoi utiliser les fonctions trigonométriques dans Excel

Pour commencer, voici quelques raisons pourquoi le choix d'Excel comme outil des calculs trigonométrique est un choix judicieux…

• Analyse Précise de Données: Excel permet de manipuler et d'analyser de grandes quantités de données rapidement. L'utilisation des fonctions trigonométriques dans ce cadre peut aider à déchiffrer des tendances complexes, à modéliser des comportements cycliques et à interpréter des données sous un nouvel angle.
• Visualisation Améliorée: Grâce à ses capacités graphiques, Excel aide à visualiser les relations trigonométriques, rendant les données plus compréhensibles et accessibles, même pour ceux qui ne sont pas experts en mathématiques.
• Applications Polyvalentes: Que ce soit pour calculer des angles dans des conceptions architecturales, analyser des oscillations en physique ou modéliser des fluctuations financières, les fonctions trigonométriques d'Excel ont une multitude d'applications dans différents domaines.
• Accessibilité et Facilité d'Utilisation: Avec une interface conviviale et des fonctions accessibles, Excel rend l'apprentissage et l'application de la trigonométrie plus faciles que jamais. Même sans une formation approfondie en mathématiques, les utilisateurs peuvent réaliser des calculs trigonométriques complexes.
• Personnalisation et Automatisation: Excel permet de personnaliser les formules et d'automatiser des tâches, ce qui est particulièrement utile pour des calculs trigonométriques répétitifs ou complexes.

En somme, Excel n'est pas seulement un logiciel de tableur; c'est un puissant outil de modélisation qui rend la trigonométrie à la fois accessible et applicable dans de nombreux contextes professionnels et académiques. Dans ce guide, je vous montrerai les fonctions trigonométriques de base et avancées, leurs utilisations pratiques et des conseils pour éviter les erreurs courantes. Que vous soyez débutant ou utilisateur intermédiaire, vous trouverez les informations nécessaires pour améliorer vos compétences en trigonométrie avec Excel.

Introduction à la Trigonométrie de Base dans Excel

La trigonométrie, cette branche fascinante des mathématiques, s'occupe des relations entre les angles et les côtés des triangles. Elle trouve ses applications dans de nombreux domaines tels que l'ingénierie, l'architecture, la physique et même l'astronomie. Pour en savoir plus sur les fondements de la trigonométrie, vous pouvez jeter un coup d'œil à l'article sur les fonctions trigonométriques sur Wikipédia..

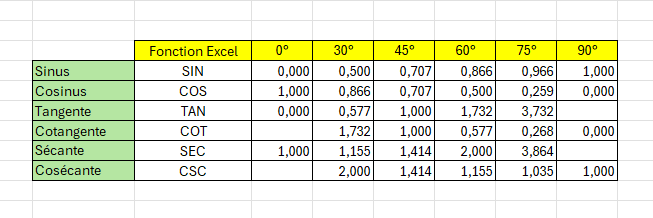
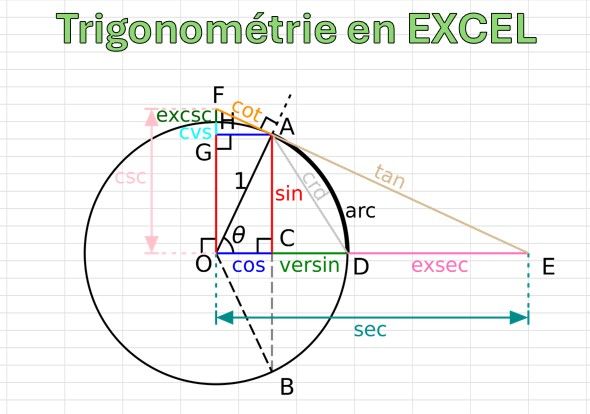
Dans Excel, l'exploration de la trigonométrie commence avec la maîtrise des "fonctions de base". Ces fonctions – COS, SIN, COT, TAN, SEC et CSC – sont les piliers sur lesquels repose l'utilisation de la trigonométrie dans le logiciel. Elles permettent de calculer respectivement le cosinus, le sinus, la cotangente, la tangente, la sécante et la cosécante d'un angle donné. Ces calculs sont fondamentaux pour comprendre les relations trigonométriques et leur application dans le traitement des données.

Fonction Excel COS (cosinus)

• Syntaxe: =COS(nombre)
• Description: Calcule le cosinus d'un angle en radians.
• Exemple: =COS(60 * PI()/180) ou =COS(RADIANS(60)) pour le cosinus de 60 degrés.

Fonction Excel SIN (sinus)

• Syntaxe: =SIN(nombre)
• Description: Détermine le sinus d'un angle en radians.
• Exemple: =SIN(45 * PI()/180) ou =SIN(RADIANS(45)) pour le sinus de 45 degrés.

Fonction Excel TAN (tangente)

• Syntaxe: =TAN(nombre)
• Description: Renvoie la tangente d'un angle en radians.
• Exemple: =TAN(30 * PI()/180) ou =TAN(RADIANS(30)) pour la tangente de 30 degrés.

Fonction Excel COT (cotangente)

• Syntaxe: =COT(nombre)
• Description: Calcule la cotangente d'un angle spécifié.
• Exemple: =COT(45 * PI()/180) ou =COT(RADIANS(45)) pour la cotangente de 45 degrés.

Fonction Excel SEC (sécante)

• Syntaxe: =SEC(nombre)
• Description: Cette fonction renvoie la sécante d'un angle spécifié en radians.
• Exemple: Pour obtenir la sécante de 45 degrés, vous pouvez entrer =SEC(45 * PI()/180) ou =SEC(RADIANS(45)).

Fonction Excel CSC (cosécante)

• Syntaxe: =CSC(nombre)
• Description: Renvoie la cosécante de l'angle donné en radians.
• Exemple: Pour calculer la cosécante de 30 degrés, utilisez =CSC(30 * PI()/180) ou =CSC(RADIANS(30)).

Comprendre et Utiliser les Fonctions Inverses Trigonométriques

Les fonctions inverses trigonométriques sont au cœur de la résolution de problèmes trigonométriques dans Excel. Elles nous permettent de déterminer les angles à partir des rapports trigonométriques connus, ce qui est essentiel dans des domaines tels que la conception, l'analyse des données et même la navigation. En d'autres termes, si on connaît la valeur d'un sinus, d'un cosinus ou d'une tangente, les fonctions inverses nous aident à retrouver l'angle d'origine.

Excel offre des fonctions dédiées pour les inverses des fonctions SIN, COS et TAN, mais ne propose pas directement des fonctions pour les inverses de la sécante (SEC) et de la cosécante (CSC). Cependant, avec une compréhension de la trigonométrie et un peu d'ingéniosité, on peut calculer ces valeurs en utilisant les fonctions disponibles.

Fonction Excel ACOS (arc cosinus)

• Syntaxe: =ACOS(nombre)
• Description: Calcule l'angle dont le cosinus est le nombre spécifié.
• Exemple: =ACOS(0,5) renvoie l'angle en radians pour un cosinus de 0,5.

Fonction Excel ASIN (arc sinus)

• Syntaxe: =ASIN(nombre)
• Description: Détermine l'angle dont le sinus est le nombre donné.
• Exemple: =ASIN(1) pour l'angle en radians correspondant à un sinus de 1.

Fonction Excel ATAN (arc tangente)

• Syntaxe: =ATAN(nombre)
• Description: Calcule l'angle dont la tangente est le nombre indiqué.
• Exemple: =ATAN(1) pour l'angle en radians avec une tangente de 1.

Pour les fonctions sécante et cosécante, bien qu'Excel ne dispose pas de fonctions inverses spécifiques, voici comment vous pouvez les calculer:

Calcul de l'ARC SÉCANTE dans Excel

• Calculé en utilisant: =ACOS(1/nombre)
• Description: Cette formule donne l'angle dont la sécante est le nombre spécifié.
• Exemple: Pour l'arc sécante de 2, utilisez =ACOS(1/2).

Calcul de l'ARC COSÉCANTE dans Excel

• Calculé en utilisant: =ASIN(1/nombre)
• Description: Fournit l'angle dont la cosécante est le nombre donné.
• Exemple: Pour l'arc cosécante de 2, saisissez =ASIN(1/2).

Applications réelles des Fonctions Trigonométriques d'Excel

Loin de se cantonner aux salles de classe, les fonctions trigonométriques d'Excel sont des outils dynamiques qui trouvent leur utilité dans de nombreux contextes professionnels. Voici quelques-unes des applications les plus frappantes…

• Architecture et Design: Les fonctions trigonométriques aident à calculer des dimensions et des angles précis dans les plans de construction, permettant aux architectes de créer des structures harmonieuses et aux designers d'optimiser l'espace et la forme.
• Analyse Financière: En finance, les cycles de marché et les oscillations des prix peuvent être modélisés à l'aide de fonctions trigonométriques pour prévoir les tendances et les comportements des investissements.
• Sciences et Ingénierie: Que ce soit pour étudier les ondes, la dynamique des fluides ou les forces structurales, les fonctions trigonométriques permettent de résoudre des équations complexes et d'analyser des données scientifiques.
• Traitement du Signal: Dans le domaine de l'électronique et de la communication, ces fonctions sont cruciales pour la modélisation et la transformation de signaux, permettant ainsi de décrypter des informations à partir de données brutes.

Ces applications pratiques ne sont qu'un aperçu de ce que vous pouvez réaliser avec une bonne maîtrise des fonctions trigonométriques dans Excel. En les intégrant dans vos feuilles de calcul, vous débloquez un potentiel d'analyse et de conception puissant et polyvalent.

Éviter les Pièges – Conseils d'Expert sur les Fonctions Trigonométriques dans Excel

L'utilisation des fonctions trigonométriques dans Excel est soumise à certaines subtilités. En tant qu'utilisateur expérimenté, j'ai constaté plusieurs erreurs courantes qui peuvent facilement être évitées avec les conseils appropriés.

• Conversion des Degrés en Radians: L'erreur la plus fréquente est d'oublier que Excel travaille en radians par défaut. Pour chaque calcul trigonométrique, assurez-vous de convertir vos angles en radians. La fonction RADIANS est là pour vous faciliter la tâche. Par exemple, =SIN(RADIANS(30)) est le moyen correct de trouver le sinus de 30 degrés.
• Gestion des Erreurs: Excel renverra une erreur si les fonctions trigonométriques sont utilisées avec des valeurs inappropriées. Par exemple, =TAN(PI()/2) provoque une erreur car la tangente de 90 degrés est indéfinie. Soyez vigilant et préparez-vous à gérer ces cas.
• Utilisation des Fonctions Inverses: Lorsque vous utilisez des fonctions inverses, assurez-vous que les valeurs sont dans le domaine correct pour éviter une erreur de type #NOMBRE!. Par exemple, =ACOS(-2) n'est pas valide car le cosinus d'un angle ne peut être inférieur à -1 ou supérieur à 1.
• Précision Numérique: Les fonctions trigonométriques peuvent parfois renvoyer des résultats qui semblent inexactes en raison de la précision numérique d'Excel. Pour des résultats plus précis, augmentez le nombre de décimales affichées.

En suivant ces conseils, vous réduirez les erreurs et augmenterez la précision de vos analyses. Les fonctions trigonométriques peuvent sembler intimidantes au début, mais avec de la pratique et une attention aux détails, vous les utiliserez avec aisance et précision dans vos projets Excel.

Conclusion – À l'Angle Droit de la Connaissance trigonométrique

Et voilà, notre immersion dans les fonctions trigonométriques d'Excel s'achève ici. Pensez à ces fonctions comme à des clés qui ouvrent les portes des calculs angulaires, prêtes à transformer les données en décisions éclairées. Excel, c'est un peu comme un super-pouvoir pour qui sait jongler avec ces outils.

Pour aller plus loin dans Excel

Et avant que vous partiez, je me permets de vous proposer quelques articles supplémentaires qui pourraient vous être utiles et rendre votre travail plus efficace…

• Liste de toutes les fonctions Excel
• Les principales fonctions Excel en détail: SI, NB.SI, SOMME.SI, RECHERCHEV, RECHERCHEH, RECHERCHEX,…
• EXCEL GRATUIT, cela vous dirait?
• Apprenez à maîtriser les Tableaux Croisés Dynamiques Excel en une heure seulement!
• Calculer l'âge actuel en Excel